< Back
BINOM.DIST function
Post
BINOM.DIST function
Description Returns the individual term binomial distribution probability. Use BINOM.DIST in problems with a fixed number of tests or trials, when the outcomes of any trial are only success or failure, when trials are independent, and when the probability of success is constant throughout the experiment. For example, BINOM.DIST an calculate the probability that two of the next three cards drawn are spades.
Syntax BINOM.DIST(number_s,trials,probability_s,cumulative) The BINOM.DIST function syntax has the following arguments:
Description Returns the individual term binomial distribution probability. Use BINOM.DIST in problems with a fixed number of tests or trials, when the outcomes of any trial are only success or failure, when trials are independent, and when the probability of success is constant throughout the experiment. For example, BINOM.DIST an calculate the probability that two of the next three cards drawn are spades.
Syntax BINOM.DIST(number_s,trials,probability_s,cumulative) The BINOM.DIST function syntax has the following arguments:
- Number_s Required. The number of successes in trials.
- Trials Required. The number of independent trials.
- Probability_s Required. The probability of success on each trial.
- Cumulative Required. A logical value that determines the form of the function. If cumulative is TRUE, then BINOM.DIST returns the cumulative distribution function, which is the probability that there are at most number_s successes; if FALSE, it returns the probability mass function, which is the probability that there are number_s successes.
- Number_s and trials are truncated to integers.
- If number_s, trials, or probability_s is nonnumeric, BINOM.DIST returns the #VALUE! error value.
- If number_s < 0 or number_s > trials, BINOM.DIST returns the #NUM! error value.
- If probability_s < 0 or probability_s > 1, BINOM.DIST returns the #NUM! error value.
- The binomial probability mass function is:
where:
is COMBIN(n,x). - If x = number_s, n = trials, and p = probability_s, then the cumulative binomial distribution is:
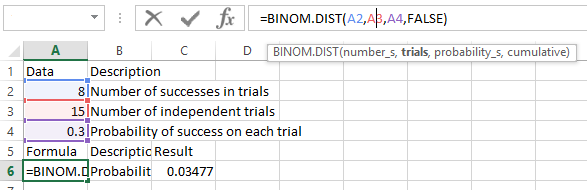
| Data | Description | |
| 8 | Number of successes in trials | |
| 15 | Number of independent trials | |
| 0.3 | Probability of success on each trial | |
| Formula | Description | Result |
| =BINOM.DIST(A2,A3,A4,FALSE) | Probability of exactly 8 of 15 trials being successful. | 0.034770014 |
