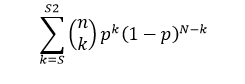BINOM.DIST.RANGE function

BINOM.DIST.RANGE function



This article describes the formula syntax and usage of the BINOM.DIST.RANGE function in Microsoft Excel.



Description Returns the probability of a trial result using a binomial distribution.



Syntax BINOM.DIST.RANGE(trials,probability_s,number_s,[number_s2]) The BINOM.DIST.RANGE function syntax has the following arguments.

• Trials Required. The number of independent trials. Must be greater than or equal to 0.
• Probability_s Required. The probability of success in each trial. Must be greater than or equal to 0 and less than or equal to 1.
• Number_s Required. The number of successes in trials. Must be greater than or equal to 0 and less than or equal to Trials.
• Number_s2 Optional. If provided, returns the probability that the number of successful trials will fall between Number_s and number_s2. Must be greater than or equal to Number_s and less than or equal to Trials.

Remarks

• If any arguments are outside of their constraints, BINOM.DIST.RANGE returns the #NUM! error value.
• If any arguments are non-numeric values, BINOM.DIST.RANGE returns the #VALUE! error value.
• The following equation is used:
  
  
• In the equation above, N is Trials, p is Probability_s, s is Number_s, s2 is Number_s2, and k is the iteration variable.
• Numeric arguments are truncated to integers.

Example Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.